High Betweenness Set Extraction
Betweenness Centrality is a useful property when searching for critical nodes in a network. The exact calculation of betweenness is however computationally expensive, which leaves us with the need for approximate methods.
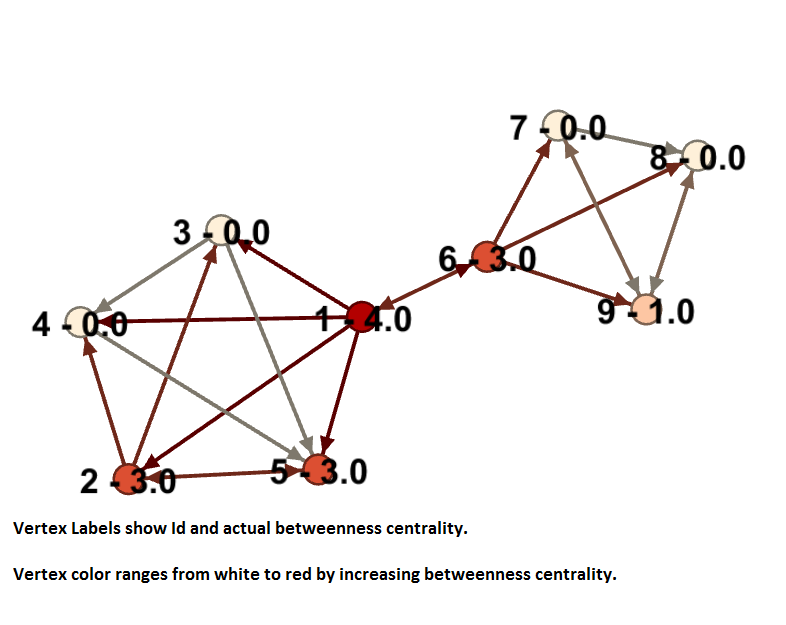
The picture above shows the approximate betweenness of the given graph. You can see some nodes are a lot more critical than others and their betweenness value reflects that.
Algorithm
- Shortest paths are calculated from a set of pivots (source nodes) to all other nodes in the graph.
- The dependency of each vertex for each pivot is calculated and added to a running total approximated betweenness.
- The highest betweenness set is extracted.
- Set stability conditions are checked. If met algorithm exits, otherwise a new pivot batch is chosen and step 1 starts again.
Benchmarks and Trade Offs
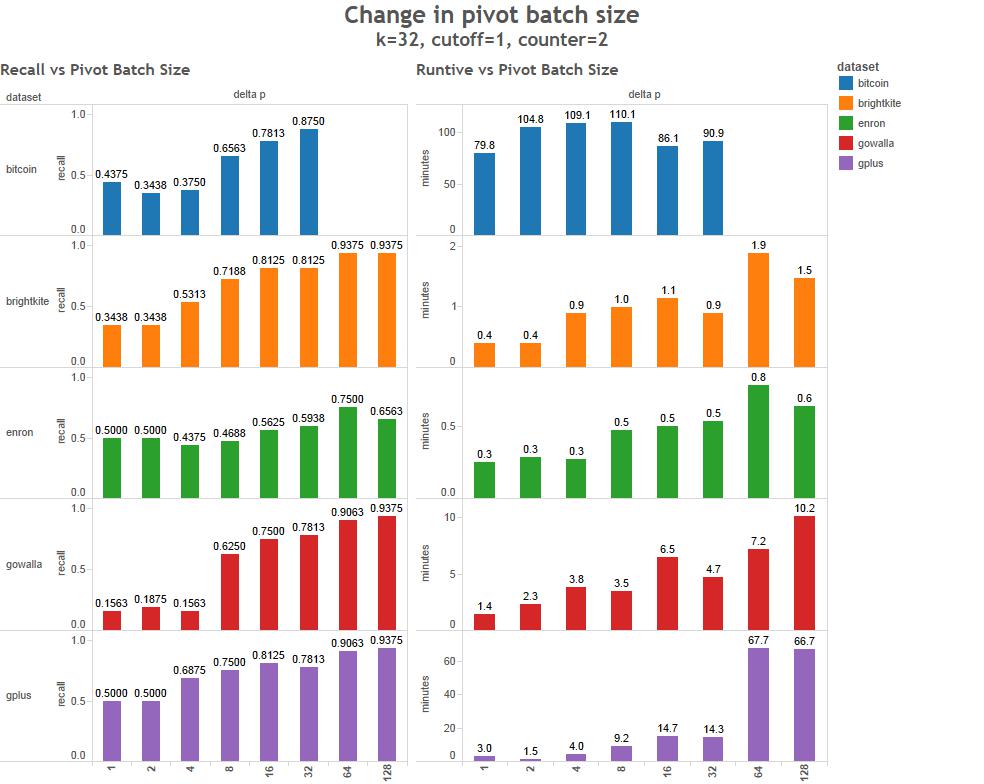
This method has 4 primary parameters that can greatly effect the run time and accuracy of the results.
- Pivot batch size - The percentage of single source shortest paths computed in parallel.
- Extracted set size - The number of high betweenness nodes to return in the result set.
- Cutoff - The threshold for membership change of the high betweenness set
- Counter - The number of times the cutoff value is reached before the algorithm exits.
To characterize the behavior of these parameters we've run a series of tests of 5 data sets.
- Bitcoin transaction graph 2,132,321 vertices 25 days to calculate exact betweenness on a single core.
- Brightkite social network. 58,228 vertices, 18 minutes to calculate exact betweenness on a single core.
- Enron email data set. 35,818 vertices, 156 seconds to calculate exact betweenness on a single core.
- Gowalla social network. 196,591 vertices (not calculated on single core)
- Google Plus social network. 102,118 vertices, 14.5 hours to calculate exact betweenness on a single core.
All tests below were run on an 8-node cluster using 8 giraph workers using 8 threads per worker.
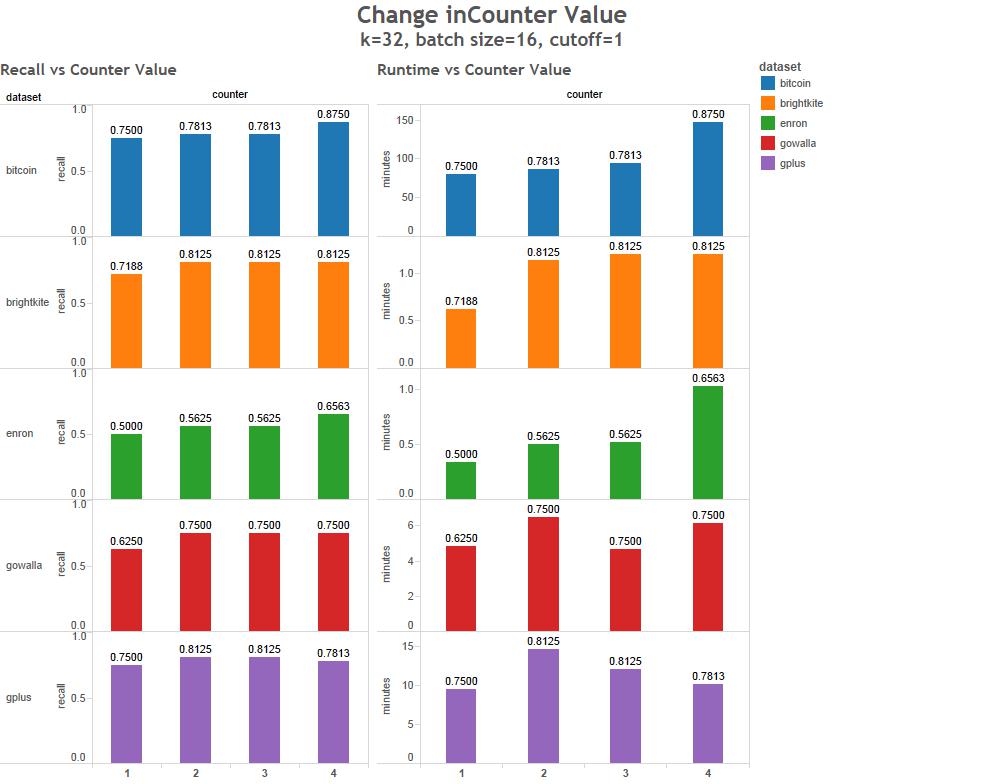
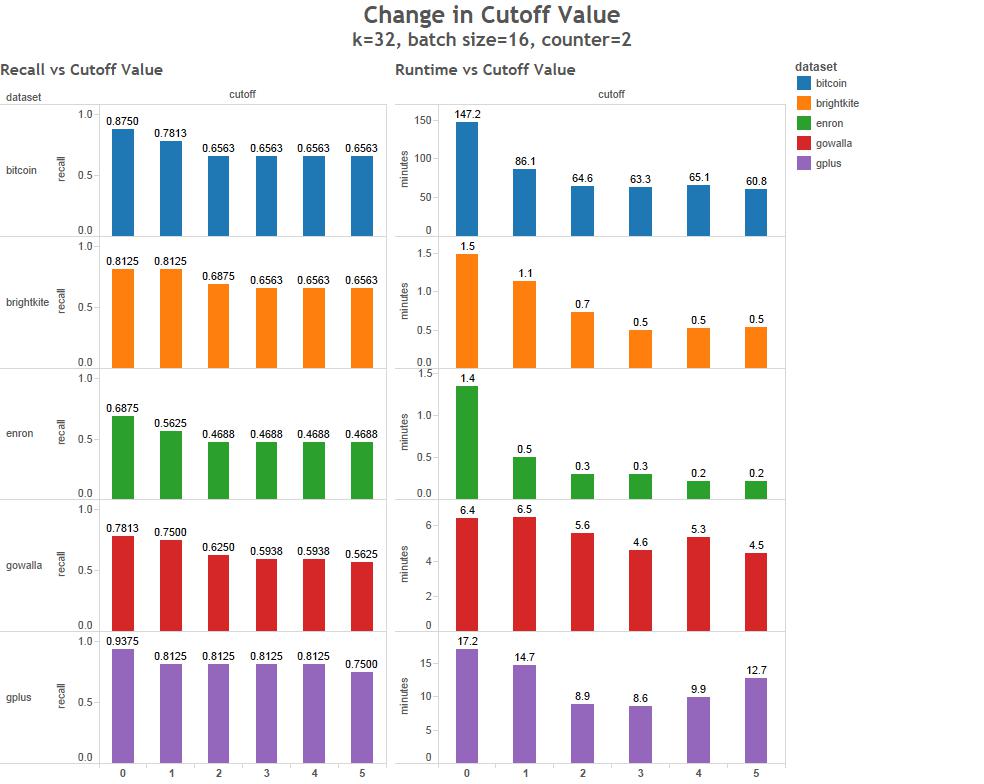
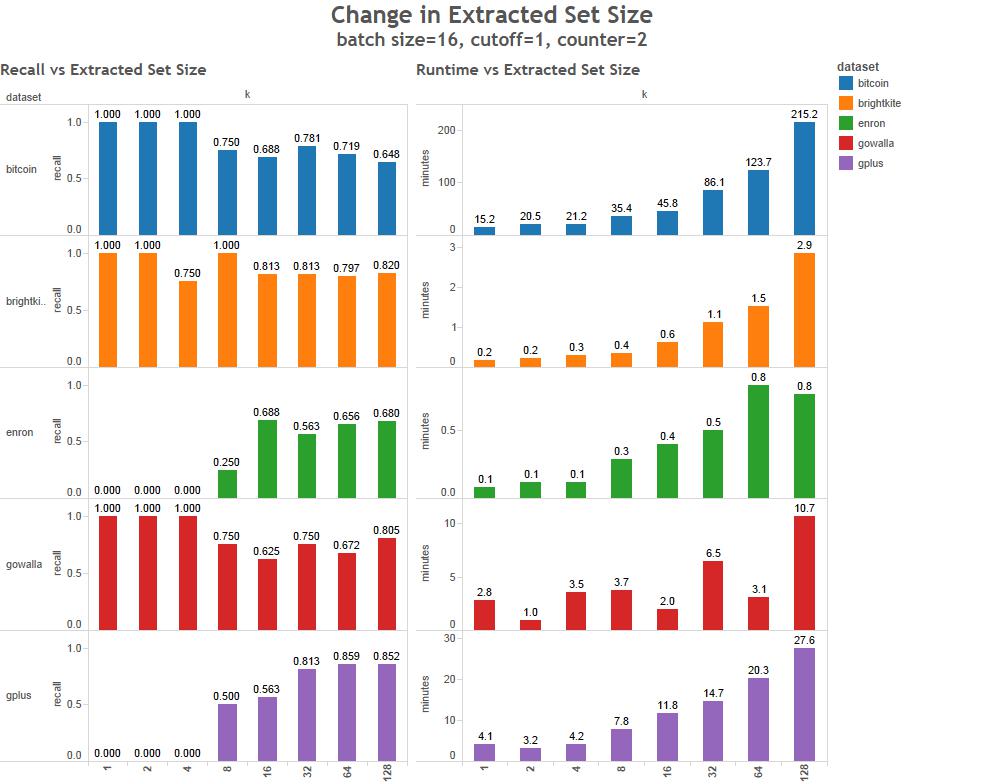
What kind of data can be used?
You can use any kind of data with HBSE. It can be directional or undirected. Keep in mind, that an undirected graph will make it even more computational heavy, thus your job will take much longer.
For background information on the approximation method see: "W. Chong, Efficient Extraction of High-Betweenness Vertices"
For background information on the method of accumulation of pair dependencies and shortest path data see: "U. Brandes, A Faster Algorithm for Betweenness Centrality"
Implementation
Our implementation is distributed using the BSP method on Apache giraph and built with Gradle. Giraph requires a Hadoop cluster (map reduce and hdfs)
I/O
The graph is read from an edge list file in HDFS, each line in the file represents a single edge and is coded as a "key,target,weight" (edge weight is optional and defaults to 1)
Output is a directory in HDFS with both the extracted high betweenness set and the approximate betweenness value for all nodes.
High Betweenness Set Extraction Configuration
| Property | Required | Description |
|---|---|---|
| betweenness.output.dir | N | Sets the betweenness set output directory. |
| betweenness.shortest.path.phases | N | Sets the number of shortest path phases that the algorithm should run through. The default is 1. |
| betweenness.set.stability | N | Sets the stability cutoff point. Defaults to 0. |
| betweenness.set.stability.counter | N | Counter for the stability cutoff point. |
| betweenness.set.maxSize | N | Sets the maximum number of nodes in a betweenness set. |
| pivot.batch.size | N | The percentage of pivots to select out of the nodes. Must be a decimal between 0.0 and 1.0. |
| pivot.batch.size.initial | N | The percentage of pivots to select initially. Must be a decimal between 0.0 and 1.0. |
| pivot.batch.random.seed | N | Seed the random number generator for pivot selection. |
| vertex.count | N | Sets the total number of vertices to perform the algorithm on. |
How To Run
Note: First see How To Build
How To Run DGA-Giraph
$ ./bin/dga-giraph hbse /path/to/input /path/to/output
How To Run HBSE with DGA-GraphX
$ ./dga-graphx hbse -i hdfs://url.for.namenode:port/path/to/input -o hdfs://url.for.namenode:port/path/to/output